Глава 4. Работа и мощность. Энергия§ 62. Равенство работ при использовании простых механизмов. «Золотое правило» механики
Рассмотренные нами простые механизмы применяют при совершении работы в тех случаях, когда надо действием одной силы уравновесить другую силу.
Естественно, возникает вопрос: позволяя получить выигрыш в силе или в пути, нельзя ли с помощью простых механизмов получить выигрыш и в работе? Для ответа на поставленный вопрос проделаем опыт.
Уравновесив на рычаге две какие-нибудь разные по модулю силы F1 и F2 (рис. 182), приводят рычаг в движение. При этом оказывается, что за одно и то же время точка приложения меньшей силы F2 проходит больший путь s2, а точка приложения большей силы F1 — меньший путь s1. Измерив эти пути и модули сил, находят, что пути, пройденные точками приложения сил на рычаге, обратно пропорциональны силам:
Рис. 182. Выигрываем в силе, но проигрываем в расстоянии
Таким образом, действуя на длинное плечо рычага, мы выигрываем в силе, но при этом во столько же раз проигрываем в пути.
Произведение силы F на путь s есть работа. Наши опыты показывают, что работы, совершаемые силами, приложенными к рычагу, равны друг другу: F1s1 = F2s2
Итак, при использовании рычага выигрыша в работе не получают.
Пользуясь рычагом, мы можем выиграть или в силе, или в расстоянии. Если мы силу приложим к длинному плечу, то выиграем в силе, но во столько же раз проиграем в расстоянии. Действуя же силой на короткое плечо рычага, мы выиграем в расстоянии, но во столько же раз проиграем в силе.
Существует легенда, что Архимед, восхищённый открытием правила рычага, воскликнул: «Дайте мне точку опоры, и я подниму Землю!»
Конечно, Архимед не мог бы справиться с такой задачей, если бы даже ему и дали точку опоры (которая должна была бы находиться вне Земли) и рычаг нужной длины.
Для подъёма Земли всего на 1 см длинное плечо рычага должно было бы описать дугу огромной длины. Для перемещения длинного конца рычага по этому пути, например со скоростью 1 м/с, потребовались бы миллионы лет.
He даёт выигрыша в работе и неподвижный блок, в чём легко убедиться на опыте (см. рис. 168). Пути, проходимые точками приложения сил F1 и F2, одинаковы, одинаковы и силы, а значит, одинаковы и работы.
Можно измерить и сравнить между собой работы, совершаемые с помощью подвижного блока. Чтобы при помощи подвижного блока поднять груз на высоту h, необходимо конец верёвки, к которому прикреплён динамометр, как показывает опыт (рис. 183), переместить на высоту 2h.
Рис. 183. Поднятие груза с помощью подвижного блока
Таким образом, получая выигрыш в силе в 2 раза, проигрывают в 2 раза в пути, следовательно, и подвижный блок не даёт выигрыша в работе.
Многовековая практика показала, что ни один из механизмов не даёт выигрыша в работе. Применяют же различные механизмы для того, чтобы в зависимости от условий работы выиграть в силе или в пути.
Уже древним учёным было известно правило, применимое ко всем механизмам: во сколько раз выигрываем в силе, во столько раз проигрываем в расстоянии. Это правило назвали «золотым правилом» механики.
Вопросы:
1. Какое соотношение существует между силами, действующими на рычаг, и плечами этих сил (см. рис. 167)?
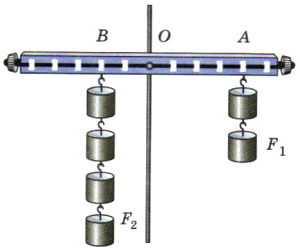
Рис. 167. Рычаг с осью вращения
2. Какое соотношение существует между путями, пройденными точками приложения сил на рычаге, и этими силами?
3. В чём проигрывают, пользуясь рычагом, дающим выигрыш в силе?
4. Во сколько раз проигрывают в пути, используя для поднятия грузов подвижный блок?
5. В чём состоит «золотое правило» механики?
Упражнения:
Упражнение № 33
1. С помощью подвижного блока груз подняли на высоту 1,5 м. На какую длину при этом был вытянут свободный конец верёвки?
2. Рабочий с помощью подвижного блока поднял груз на высоту 7 м, прилагая к свободному концу верёвки силу 160 Н. Какую работу он совершил? (Вес блока и силу трения не учитывать.)
3. Как применить блок для выигрыша в расстоянии?
4. Как можно соединить друг с другом неподвижные и подвижные блоки, чтобы получить выигрыш в силе в 4 раза; в 6 раз?
5. Решите задачу 2, учитывая вес блока, равный 20 Н.
Задания:
Докажите, что закон равенства работ («золотое правило» механики) применим к гидравлической машине. Трение между поршнями и стенками сосудов не учитывайте.
Указание.
Используйте для доказательства рисунок 144.
Рис. 144. Принцип действия гидравлической машины
Когда малый поршень под действием силы F1 опускается вниз на расстояние h1, он вытесняет некоторый объём жидкости. На столько же увеличивается объём жидкости под большим поршнем, который при этом поднимается на высоту h2.
Предыдущая страницаСледующая страница
Задачи на простые механизмы с решениями
Формулы, используемые на уроках «Задачи на простые механизмы,
условия равновесия рычага, блоки, золотое правило механики».
Задача № 1.
С помощью рычага рабочий поднимает плиту массой 120 кг. Какую силу он прикладывает к большему плечу рычага, равному 2,4 м, если меньшее плечо 0,8 м?
Задача № 2.
На концах рычага действуют силы 20 Н и 120 Н. Расстояние от точки опоры до большей силы равно 2 см. Определите длину рычага, если рычаг находится в равновесии.
Задача № 3.
На рисунке изображен рычаг, имеющий ось вращения в точке О. Груз какой массы надо подвесить в точке В для того, чтобы рычаг был в равновесии?
Задача № 4.
На меньшее плечо рычага действует сила 300 Н, на большее — 20 Н. Длина меньшего плеча 5 см. Определите длину большего плеча.
Задача № 5.
Рычаг длиной 60 см находится в равновесии. Какая сила приложена в точке В?
Задача № 6.
Момент силы действующей на рычаг, равен 20 Н*м. Найти плечо силы 5 Н, если рычаг находится в равновесии.
Задача № 7.
Какое усилие необходимо приложить, чтобы поднять груз 1000 Н с помощью подвижного блока? Какая совершится работа при подъеме груза на 1 м? (Вес блока и трение не учитывать).
Задача № 8.
Система блоков находится в равновесии. Определите вес правого груза. (Вес блоков и силу трения не учитывать).
Задача № 9.
При помощи подвижного блока поднимают груз, прилагая силу 105 Н. Определите силу трения, если вес блока равен 20 Н, а вес груза 180 Н.
Задача № 10.
ОГЭ
Стержень цилиндрической формы длиной l = 40 см состоит на половину своей длины из свинца и наполовину — из железа. Найти расстояние от центра тяжести до центра симметрии стержня. Плотность свинца p1 = 11,4 г/см3, плотность железа p2 = 7,8 г/см3.
Решение. Центр тяжести тела (центр масс) — точка приложения силы притяжения его к земле — веса тела P. У тел, имеющих какую-либо симметрию, он совпадает с центром симметрии. Например, у однородного цилиндра центр тяжести расположен на его оси в центре цилиндра. Тело, закреплённое на оси, проходящей через его центр тяжести, находится в состоянии безразличного равновесия. Мысленно закрепим стержень AB на оси, перпендикулярной стержню и проходящей через его центр тяжести C, отстоящий от его геометрического центра O на расстояние x в сторону более тяжёлой половины стержня. Центры инерций половинок размещены на расстояниях l/4 от середины стержня.
х = (11,4–7,8)/(11,4+7,8) • 0,4/4 = 0,01875 ≈ 0,019 (м)
Ответ: 1,9 см.
Задача № 11.
ЕГЭ
Масса якоря корабля m = 50 кг. Радиус барабана, на который наматывают якорную цепь, R = 0,2 м, длина каждой из двух ручек ворота l = 1 м. Какую силу нужно приложить к каждой из них, чтобы поднять якорь?
Упражнения
Упражнение №1
Рабочий с помощью рычага поднял груз массой $150 \space кг$. Приложенная им сила совершила работу в $300 \space Дж$. На какую высоту рабочий поднял груз? Сделайте чертеж.
Изобразим графически данный рычаг (рисунок 5).
Рисунок 5. Чертеж к упражнению №1
AB — рычаг с точкой опоры O. $F_1$ — сила тяжести груза, $F_2$ — сила, приложенная рабочим. $l_1$ и $l_2$ — плечи сил. Отрезок AD — это высота, на которую рабочий понял груз ($AD = h_1$), отрезок $BC$ — высота, на которую рабочий опустил длинное плечо рычага ($BC = h_2$).
Дано:$m = 150 \space кг$$A_2 = 300 \space Дж$$g = 9.8 \frac{Н}{кг}$
$h_1 — ?$
Показать решение и ответ
Скрыть
Решение:
При использовании рычага выигрыша в силе не получают: $A_1 = A_2$.
Работа, совершаемая силой, приложенной к грузу:$A_1 = F_1s = F_1h_1$
Выразим высоту, на которую поднят груз:$h_1 = \frac{A_1}{F_1} = \frac{A_2}{gm_1}$,$h_1 = \frac{300 \space Дж}{9.8 \frac{Н}{кг} \cdot 150 \space кг} \approx 0.2 \frac{Н \cdot м}{Н} = 0.2 \space м$.
Ответ: $h_1 = 0.2 \space м$.
Упражнение №2
С помощью подвижного блока груз подняли на высоту $1.5 \space м$. На какую длину при этом был вытянут свободный конец веревки?
Дано:$h = 1.5 \space м$
$l -?$
Показать решение и ответ
Скрыть
Решение:
Подвижный блок дает выигрыш в силе в 2 раза. Тогда по «золотому правилу» механики, будет проигрыш в пути в 2 раза:$l = 2h$,$l = 2 \cdot 1.5 \space м = 3 \space м$.
Ответ: $l = 3 \space м$.
Упражнение №3
Рабочий с помощью подвижного блока поднял груз на высоту $7 \space м$, прилагая к свободному концу веревки силу $160 \space Н$. Какую работу он совершил? (Вес блока и силу трения не учитывать.)
Дано:$h = 7 \space м$$F_2 = 160 \space Н$
$A_2 — ?$
Показать решение и ответ
Скрыть
Решение:
Работа, совершаемая рабочим:$A_2 =F_2 s_2 = F_2 h_2$.
При использовании подвижного блока мы получаем проигрыш в пути в 2 раза:$h_2 = 2 h_1$.
Рассчитаем работу, совершенную рабочим:$A_2 = F_2 \cdot 2 h_1$$A_2 = 160 \space Н \cdot 2 \cdot 7 \space м = 2240 \space Дж = 2.24\space кДж$.
Ответ: $A_2 = 2.24 \space кДж$.
Упражнение №4
Как применить блок для выигрыша в расстоянии?
Посмотреть ответ
Скрыть
Ответ:
Используя подвижный блок, мы тянем за свободный конец веревки. Так мы получаем выигрыш в силе, но проигрываем в пути (расстоянии).
Соответственно, чтобы получить выигрыш в расстоянии, мы должны прикрепить груз к прежде свободному концу веревки, а силу ($F_2$) прикладывать к оси блока (рисунок 6).
Рисунок 6. Использование подвижного блока для получения выигрыша в расстоянии
Теперь при перемещении оси блока на расстояние $s_2$, груз переместится на расстояние $s_1 = 2 \cdot s_2$.
Упражнение №5
Как можно соединить друг с другом неподвижные и подвижные блоки, чтобы получить выигрыш в силе в 4 раза; в 6 раз?
Посмотреть ответ
Скрыть
Ответ:
Чтобы получить выигрыш в силе в 4 раза, в конструкции должны быть 2 подвижных блока, соединенных друг с другом (рисунок 7). Каждый их них дает выигрыш в силе в 2 раза, а в сумме они дадут требуемый выигрыш в силе в 4 раза.
Рисунок 7. Комбинация блоков, дающая выигрыш в силе в 4 раза
По такой же логике для получения выигрыша в силе в 6 раз нам понадобится 3 подвижных блока (рисунок 8).
Рисунок 8. Комбинация блоков, дающая выигрыш в силе в 6 раз
Упражнение №6
Решите упражнение №3, учитывая вес блока, равный $20 \space Н$.
Дано:$h = 7 \space м$$F_2 = 160 \space Н$$P = 20 \space Н$
$A — ?$
Показать решение и ответ
Скрыть
Решение:
Общая работа по поднятию груза и подвижного блока, совершенная рабочим, будет равна:$A = A_1 + A_2$.
Работа по поднятию груза:$A_1 = F_2 s_2 = F_2 h_2$.
При использовании подвижного блока мы получаем проигрыш в пути в 2 раза:$h_2 = 2 h_1$.
Тогда работа по поднятию груза будет равна:$A_1 = F_2 \cdot 2 h_1$.
Работа по поднятию блока:$A_2 = P h_1$.
Теперь мы можем рассчитать общую работу:$A = F_2 \cdot 2 h_1 \space + \space P h_1 = h_1 (2 F_2 \space + \space P)$,$A = 7 \space м \cdot (2 \cdot 160 \space Н \space + \space 20 \space Н) = 7 \space м \cdot 340 \space Н = 2380 \space Дж = 2.38 \space кДж$.
Ответ: $A = 2.38 \space кДж$.
Задание
Докажите, что закон равенства работ («золотое правило» механики) применим к гидравлической машине. Трение между поршнями и стенками сосудов не учитывайте.Используйте для доказательства рисунок 9. Когда малый поршень под действием силы $F_1$ опускается вниз на расстояние $h_1$, он вытесняет некоторый объем жидкости. На столько же увеличивается объем жидкости под большим поршнем, который при этом поднимается на высоту $h_2$.
Рисунок 9. Принцип действия гидравлической машины
Посмотреть доказательство
Скрыть





























